WonderWitch でプログラミングをしていると、やっぱりハードの制限もあって、
CPU パワーにモノを言わせてゴリゴリ演算とかができません。
浮動小数点演算もその 1 つで、i486DX より前の CPU では鬼門の一つでした。
で、WS の CPU も公称では 80186 コンパチで、勿論コプロは付いてません。
故に、浮動小数点演算が遅いのは当たり前と言えば当たり前なんですが、
まさかこれほどまでに遅いとは思わなかった訳です。
簡単なテストなんですが、「sum」「d」を float 型にしたときと int 型にしたときで、 どのくらいの速度差が出るか、WW で走らせてみて下さい。演算を行っている間は LCD が消えます。 やたら長い間 LCD が消えてたりしますが、別にフリーズしてるわけではありません。
/* WonderWitch じゃないと走んないけど */
#include <sys/bios.h>
void main( void )
{
int sum = 0, d = 2; /* どちらかをコメントアウト */
/* float sum = 0, d = 2; */
int i;
lcd_off();
for( i = 0 ; i < 20000 ; i++ )
sum += d;
lcd_on();
}
LCD が消えているのは、int のときは 0.3 秒程度、float の時はなんと約 6 秒。
時間にして約 20 倍。開発者の話では「足し算とかは 1clock」
ということですから、浮動小数点の足し算 1 回で、最低でも
20clock 掛かってる計算になります。
実際には、int のときの「0.3 秒」の大半は
LCD 操作に費やされてるでしょうから、もっと掛かってるはずです。
float のときの時間の長さからすれば、
LCD 操作のオーバーヘッドは無視できる程度ですから、
それを踏まえて計算すると、1 ループで
3*10^6[Hz] * 6[s] / 20000[回] = 900[clk] 。
仕方ないのは分かってますが、はっきり言って遅すぎます。
で、この遅いのをどうにかしようということで、固定小数点を使うわけです。

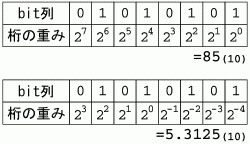
学校で 2 進数の勉強をした人なら分かると思いますが、 コンピュータでの数値の内部表現はこんな感じです。図 (a) 上の例なら、 26 + 24 + 22 + 20 で、 85(10)となります。
で、これを図の下の例のように「見なして」みることで、 固定小数点変数が実現できます。「表現できる数の、レンジを狭く、精度を高く」 するわけです。私はこの概念が理解できなくて 6 時間ほど悩みました(苦笑
この例なら、 22 + 20 + 2-2 + 2-4 で、 5.3125(10) となります。101.0101(2) ですね。
固定「小数点」とは言っても、「固定」なわけですから、
浮動小数点みたいに符号部だ仮数部だ指数部だと考える必要はありません。
要は、小さい数に下駄を履かせて (整数倍して)、無理矢理整数で表すわけです。
固定小数点を表す型 (仮に fixpoint 型とする) には、「ビット演算ができる型」から、
「十分な数の範囲と精度が得られる」bit 数の型を選んで typedef します。
固定小数点変数への代入ですが、例えば上のテーブルの例なら、
fixpoint f = 3 << 4;または
fixpoint f = 3 * 16;とすると、f に 3 (を表すビット列) が代入されます。
C 言語には算術シフト演算子なんてものは無いので、符号付き数を扱う場合はシフトでなく乗除算を使う必要があります
(シフトすると最上位の符号ビットまでシフトされてしまうため、値がおかしくなる)。
WS の CPU が巷で噂のアレだとすると、乗除算命令は非常に高速に実行できる (専用ユニットがある) らしいので、
後者でも速度的には問題無いでしょう。勿論、符号無し数を扱う場合には、前者を用いた方が速度的は断然有利です。
あと、浮動小数点変数には (一応) ビット演算ができない (ことになっている) ので、これも後者で処理します。
で、逆に、整数として取り出したい場合は、
int i = f >> 4;または
int i = f / 16;とすれば OK です。小数部まで取り出したい場合は、16.0 (実数) で割れば OK です。ここで、 ( float )( f / 16 ) では意味が無いし、( float )f / 16 は上手く動かない事があるようなので注意が必要です。
式の中にシフト演算子が沢山出てきてイヤーソという場合は、
#define FIX_POWER 64 /* 固定小数点のアレ */
#define int2fix( x ) ( ( x ) * FIX_POWER )
#define fix2int( x ) ( ( x ) / FIX_POWER )みたいなマクロを組むと分かり易くて吉かと思います。勿論、FIX_POWER は、 必要な精度と数の範囲に応じて決めます。この例なら、精度は最大で 1/64 ですね。 10/3 の結果は 3.3285 位になります。なんだかバグ入りペンティアムを彷彿とさせますが、これで正しいのです(笑
あとは演算です。加減算は、オペランドを固定小数点にキャストして、後は普通に行えば OK です。 乗除算は、整数・浮動小数点との演算はそのまま行って構いません。
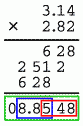
問題は固定小数点同士の乗除算です。 小学校で習った「筆算」を思い出して貰えれば分かり易いと思いますが、 小数点の位置が変わるため、それを考慮する必要があります。
図 (b) は、3 桁の固定小数 BCD (うわぁ) で考えてみたものです。
そのまま下位 3 桁 (赤で囲んだ部分) だけで計算すると、上位桁が格納できず、
「548」という意味不明な答えになってしまいます。
正答 (青で囲んだ部分) を得るためには、倍の桁数が格納できる BCD 変数を用意して (緑色で囲んだ範囲)、
その変数内で計算を行い、小数点のずれた桁数を考慮して、正しい位置から 3 桁を抜き取ります。
この場合、2 つの数とも小数部は 2 桁ですから、最下位 2 桁を切って、そこから下位 3 桁を答えとして得るわけです。
本当なら、消える桁を四捨五入するなどの処理が必要なのかも知れませんが、まぁ面倒なのでやっていません。
ちなみに四捨五入の仕方は、小数第 1 位を四捨五入するなら「0.5 を足して切り捨て」ですね。
実装としては、
typedef int fixpoint;
fixpoint multiply( fixpoint x, fixpoint y ) /* x * y */
{
return ( ( long )x * ( long )y ) / FIX_POWER;
}
fixpoint divide( fixpoint x, fixpoint y ) /* x / y */
{
return ( ( long )x * FIX_POWER ) / ( long )y;
}といった感じになります。
掛け算では、上で示したように、小数点の位置が左に移動して、上位桁が消えてしまうので、
サイズが倍の型に代入してから掛け合わせて、そこから結果を抜き取ります。
逆に割り算では、小数点の位置が右に移動して、下位桁が消えてしまうので、型キャストの後、
被除数にあらかじめ下駄を履かせておいて、小数点の位置を補正すると共に精度を保たせます。
割り算が「( ( long )x / ( long )y ) * FIX_POWER;」では無いことに注意して下さい。
こうすると小数部がつぶれてしまいます (10/3 が 3.328…… ではなく 3.00…… になってしまう) 。
ネタはやっぱりパクりです。チャーパーさん、御免なさい。(苦笑)
勿論、固定小数点自体は昔から使われていたモノなんですけどね。
「ブロックで某」でこの固定小数点というモノを使っているわけですが、浮動小数点を使うと、 球を 8 つ出した時点で処理落ちが始まったのに対し、固定小数点を使った場合では、 50 個出しても全然平気でした。やってるのは加減算だけですが、凄いぞ固定小数点。