数学の教室
研ぎ澄ませ、己が感性を。ア・プリオリに数学は理解可能だ。純然たる
自然との関わりの中において、人は数学を己が内に息づかせることができる。
目覚めさせよ、今は眠りし数学の魂を！
＜虚数(imaginary number)＞
正直言えば、この命題を解説するのにこのスペースは狭すぎる。
が、質問があった以上それなりの回答を示していく。頭で考えるのではなく、
感性によってイメージスキーマを構築することを切に願う。
一言で言ってしまえば「虚数とは自乗してマイナスの値となる数値」の事だ。
しかしながら、x2（xは任意の実数）>= 0という性質（定義）があり、
これはxがプラスであろうとマイナスであろうと必ず成立するものだ。
実質的な内容は持たず、数学などの便宜上作り出された数であり、
それ以上でもそれ以下でもない。従って虚数とは何か、と言われれば
上記のように答えるしかないのである。
歴史的に見ても古代ギリシアや古代インドでは「自乗してマイナスになる数は
除く」という決まりがあった。しかしながら、これを逆に考えれば当時の者は
「自乗してマイナスになる数」という概念自体は持っていたことになる。
結局諸々の事情（虚数解を認めることで、３次方程式の実数解も得やすくなる
ということなど）によって虚数は数学の中でその地位を獲得する。
（なお、虚数を表す記号は、数学では i である。）
とは言うものの、虚数はあくまで実世界には存在しない範疇のいわば想像上の
数字である。しかし、電気工学や数学の世界では、この概念がなければ
うまく理論を形成できない事もあり、いわば便宜上作り出された数字であると言える。
これをどう捉えるかは各個人の判断にゆだねるが、実数(real number)と言えども
それ自体が現実世界に姿をもって存在しているものではなく、現実の何かを表現するのに
都合がいいから発明されたものであることを考えれば、虚数も素直に受け入れられるのでは
ないであろうか？さらに、虚数が現実の何をも表現し得ないという性質ながら、
数学的に認識されているということは、人間の想像力が素晴らしいということにもなる。
さながら混乱を来すとするならば、x2>= 0 という定義に反するためであろう。
これを単なる実数と虚数との境界と考えればしっくりくるのではないだろうか？
たとえば正の数と負の数との境界は０より大きいか小さいかだ。しかし両方とも
実数だ。これと同じように実数と虚数との境界がx2>= 0であり、
両方とも数（広義の複素数）だ。双方ともに基本的な数学的正確は共有している。
ならば虚数を自然と受け入れられるようになると思うのだが。
もっと考えやすくする。虚数には大小関係がない。と、その説明をする前に
複素数について説明する。a+biの形で表せるものを「複素数」といい、すべての
数は複素数である。つまりa is not 0 かつ b = 0 ならば「実数」、その逆ならば
「純虚数」、a,b共に０以外の実数ならば「狭義の複素数」となるのである。
さて、この複素数を視覚的に捉えるにはどうすればよいか？実数は数直線という
仮想直線上に列挙できる。しかし虚数はこの数直線上に存在しない。ではどこに
表記すればよいのか？これに対して答えを出したのが私の兄弟子である大数学者
ガウスである。
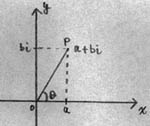ガウスは右図のような座標系を考案。ここに全複素数を書くことができるように
したのである。（この座標系を「ガウス平面」「複素数平面」という。）
x軸を実数軸、y軸を虚軸といって、それぞれ実数と純虚数を表せる。
これらの組み合わせの交点で複素数を表現するのである。この平面上で
図形的に四則演算を行うことも可能だが、スペースの都合上割愛する。
たとえばa+biという数は、右図の点Ｐに表せる。さらにこの複素数の
絶対値はroot(a2+b2)となる。ただしこの絶対値は
実数の絶対値とは異なるものなので、単純に双方を比較して、どちらが
大きいかなどの考察はできない。
これからP0xで表される角度をθとし、上記の絶対値をrとした場合、
a+bi=r(cosθ+isinθ)と表せる。
かように視覚的に虚数が表現できることで、虚数が身近に感じられるように
なったのではないだろうか。
うーむ、いまいち理論的になってしまった。次からはもっと感覚的に
説明する事を目標にする。