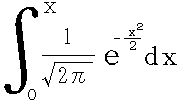数学ガイダンス原稿
(いつこの原稿を書いたかなんて覚えてねー。ページ作成は2006/10/29)
確認事項、連絡事項等
(科目名、クラスの確認、再履に対する注意)
(自己紹介、TAがいれば紹介)
(この時間はガイダンスをやる旨の説明、及び工学部教官の紹介)
(合否の判定などについて適当に)
・質問は大歓迎です。
そうは言っても、質問というのもなかなか難しい。
質問というのは「自分は何が分かってないのかを言葉で説明する」ことですから、
「何が分かってないか」が分かってないと質問のしようがない。
でもそれが分かるくらいなら、問題の半分以上は解決したようなものです。
それが分からないから困る。
「アメリカ人はよく質問をする」といいますが、あれは
「何が分かってないか分かっている」から質問が出来るわけじゃなくて、
「なんだか良く分からないけどとりあえず質問してみて、
相手との掛け合いの中で問題点をはっきりさせていく」
という事をやってるんだと思います。
もちろん「自分の頭の中で問題点を整理する」事も大事ですが、
「掛け合いの中で問題点をはっきりさせる」事も大事。
そういう意味で「質問は大歓迎」です。
ガイダンスのイントロ
今日のガイダンスでは、この授業が「基礎科目」という事で、
今後の専門科目を学ぶ上で必要な科目なのですが、
「何を学ぶのか」(簡単に言ってしまえば微分積分の拡張なのですが)、
「それが今後の専門にどのように関係するのか」についてお話します。
とはいえ、工学部ならば、紀伊国屋、旭屋、三省堂、ジュンク堂辺りに行って、
工学書コーナーのそれっぽい本を開いてみれば数式が並んでますから、
必要性はなんとなく感じているでしょう。
最近では理工学でなくても、例えば文学でさえも、小説を全部コンピュータにぶちこんで、
統計的手法を用いて新しい発見はないかと研究する「計量言語学」という分野もあるくらいです。
大企業の中には広告の打ち方と売上の関係を数学的に調べている所もあります。
工学の例については後ほど(工学部教官名)先生にお話して頂くので、工学以外の例を挙げてみます。
このページを見てください。
これは「保健」と「保険」に関係するものですが、「平均寿命」の定義が書かれているページです。
「日本人の平均寿命は世界一」などと言いますが、その「平均寿命」とはどんな意味を持ち、
どう計算するのかを手短に説明しているものです。
平均寿命をもうちょっと拡張した概念が下の方にある「平均余命」ですが、
それを定義するのに「定常人口」が必要、その「定常人口」を定義するのに積分が使われている。
このように、微分積分やその他の数学は、単に計算するだけでなく、
このように意味や概念を説明したり定義したりするのにも使われます。
場合によってはそっちの方が多いくらいです。
工学では忙しい人も多いので、簡単な加減乗除だけで結果が出るような便利な実用書もたくさんあるのですが、
その式が意味するもの、あるいは背景を理解するためには微分積分を理解している必要があります。
さて、この講義は「解析学」といいますが、最初のうちは微分積分と思っていて大丈夫です。
しかし後になると「2次元以上の微分積分」をやりますので、
もうひとつの数学科目である線型代数の知識も関係してきますので、両者きちんと勉強して、
両者の関係にも注目してください。
では、高校までの微分積分、あるいは数学となにが違うのか?
より複雑な計算ができるようになる
これは誰でも考えるところでしょう。出来るだけ難しい問題が解けるようになりたい。
しかし次の積分を見てください。
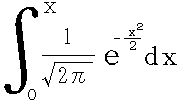
この積分は統計で頻繁に出てくる積分ですが、
これはXの多項式、分数、累乗根、指数関数、対数関数、三角関数の組み合わせでは書けません。
難しくてまだ誰も出来ていない、というのではありません。理論上どんなにがんばっても出来ないんです。
よく知ってる加減乗除、累乗根、指数関数、対数関数、三角関数では表現出来ない。
さてどうしよう?(と、ここで学生につっこむ)
区分積分法で計算するんでしたね。区間を無限に小さくすれば積分が求まる。
しかし現実には「無限」なんて出来ない。人間も計算機も有限回しか出来ない。
所詮、近似計算な訳です。もちろん自分の必要とする精度まで近似をしなければならない訳ですが、
理論的に出来ない事がある、では逆に自分が何を必要として何をやればいいのか、という事も考える必要がある訳です。
その辺の見極めが出来るようになって欲しい。
一般化・抽象化
この言葉は数学でよく表れる言葉です。これを、もうひとつの数学科目である「線型代数」を例に説明してみましょう。
ところで、「比例」ってなんですか?小学校で習った「比例」です。(と学生につっこむ)
「ある a によって y=ax と書ける x と y の関係」(no.01)
でした。でも小学校で一番最初に比例が出てきた時には、こんな事もやったと思います。
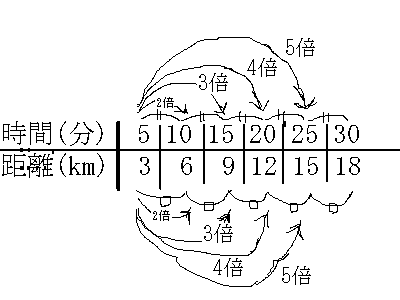
まずこんな表を書いた。そして、
時間が2倍になると距離が2倍、時間が3倍になると距離も3倍。
あるいは、時間の間隔が等しいと、対応する距離の間隔が等しい。
こういった性質を大学生風に書くとこうなります。
「どんな実数 a,x,y に対しても f(ax)=af(x), f(x-y)=f(x)-f(y)が成り立つ関数 f(x)」(no.02)
(no.01)の形に書ける関数は(no.02)が成り立つ。逆に(no,02)が成り立つ関数は必ず(no.01)の形に書ける。
どちらを比例の定義にしてもいいんだけど、ここでは(no.02)を比例の定義だと考えよう。
さらに x,y を実数でない他のものにまで拡張して、この「比例」の概念(no.02)を考えてしまおう(一般化)。
とはいえ、(no.02)の文章の中には「実数倍」と「足し算・引き算」があるので、
実数倍と足し算・引き算がある集合でないと意味がない。そういう集合 M を「ベクトル空間」といい、
M での「関数」で(no.02)が成り立つものを線型写像または一次写像といいます。
そんなこと言っても、そういう集合が実際になければ意味がない。でもちゃんとあります。たくさんあります。
(a)数ベクトル空間(n個の実数の組(a1,a2,…,an)の全体の集合)
足し算は対応する成分ごとに足し算、実数倍は全ての成分を同じ数で掛け算する。これでベクトル空間になる。
この時、n行列 A をかける事が線型写像になっている。
(b)平面ベクトル全体の集合。
足し算は平行四辺形の対角線で定義、実数倍は同じ向きで長さを実数倍(負の場合は逆向き)。これでベクトル空間になる。
この時、回転操作が線型写像になっている。
(c)微分可能な関数全体の集合。
2つの微分可能な関数を普通に足し算したり実数倍すれば、やはり微分可能な関数になるので、これでベクトル空間になる。
この時、微分操作が線型写像になっている。
他にもあるんですが、「線型代数」というのはどのベクトル空間にでも成り立つ理論である、というのが「抽象化」です。
同じ文章の定理が(a)でも(b)でも(c)でも他のものでも、ベクトル空間でありさえすれば何にでも成り立つ。
線型代数を具体的な例で考える事も、勉強方法としてはとても大事な事です。
平面ベクトルや空間ベクトルなどの図形は非常に分かりやすい例なので、とても便利です。
しかし図形ベクトルでは3次元以上のものは考えられない、という欠点がある。
工学では100次元の方程式を解くなんてよくある話ですから、図形だけでは理解不可能になる。
(c)の微分可能関数のベクトル空間に至っては無限次元です。
理学工学などでよくある話で、目の前の問題が、実はベクトル空間で、線型代数使えば簡単に解けるのに、
その事に気づかず延々と悩み続ける、なんて事があります。教科書に載っている例だけではなく、
他にベクトル空間になるものはないか、他に微分積分を応用できるものはないか、探し出すくらいの気持ちで勉強してください。
ところで(a),(b),(c)の線型写像は、元々は「比例」の拡張、一般化でした。つまり「関数」の一般化です。
(a)の一定の行列を掛けるという「関数」はまだいいんですが、
(b)の回転操作も「関数」の拡張、(c)の微分操作も「関数に対して関数が決まる『関数』」です。
関数を1個のモノのように考えて「関数の関数」を考える事は、数学だけでなく物理学(量子力学)などで現れます。
この辺にも慣れてください。
色々といいましたが、そうは言っても微分積分の延長ですから、そんなに難しいわけじゃない。
でも教科書を開くと、なんとなく難しそうだ。なぜか。
専門用語、専門的文章、専門的な言い回し
この手の本が難しそうに見えるのは、専門用語や専門的な言い回しに慣れていない、というのが大きな原因です。
理系文系問わずそうなんですが、難しい言い回しで言ってるけども、実は無茶苦茶簡単な内容である事が少なくない。
なんで簡単な事を難しい言い回しで言うのか、それはそれなりに理由があるんですが、見掛け倒しな事も少なくない。
特に長い文章に根負けする人も多いんですが、そういった文章に慣れて、「これは本質的には簡単な事」「これは本当に難しい事」
と見分けられるようになると、勉強もはかどります。
また、同じ言葉が違う分野で別の意味で使われたり、逆に同じ事を分野によって別の言葉で表現したりと、
混乱させられる事も多いんですが、そういった事も慣れてくると、
今まで自分が勉強した事のない分野を新しく勉強する時にスムーズに頭に入ります。
いろんな分野の本を読んで、専門的な言い回しに慣れてください。