Data & Algorithm 今回のお題：
『ソート (2) - シェーカーソート、シェルソート、マージソート』

●概要

ソートの 2 回目は、「割と高速なソート」にも手を伸ばしていきます。

1. シェーカーソート

バブルソートを一寸だけ弄ったアルゴリズムです。 やはりソートされていく様子からその名が付きました。 「遠心分離器ソート」と言った方がしっくりくるかも。

バブルソートは常に「左から右」へ詰めていって、 右端からソート済みの部分が伸びて行くわけですが、 シェーカーソートは、ソート済みの部分を「両端から」伸ばしていきます。 つまり「左から右」へバブルソートを掛けて、次は「右から左」 へバブルソートを掛けて……の繰り返しになるわけです。 バブルソートと比べて、速度がデータの状態や内容に左右されにくく、 常に安定した速度で動作する……らしいです。

さらに、高速化を図るため、簡単なチェックを掛けてみました。 このアルゴリズムでは、「最後に交換が起こった場所以降」 のデータはソート済みであることが保証されているわけですから、 その場所を記憶して、それ以降は見に行かないようにしてあります。 このチェックは、バブルソートにも利用できます。

2. シェルソート

挿入ソートを弄ったアルゴリズムです。Shell さんが考えたからシェルソート、 らしいです。

挿入ソートの特徴として、

といったものがありますが、これを利用しています。

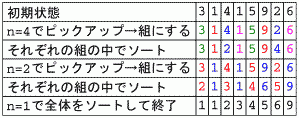
で、このソートですが、基本的には「n だけ離れた要素間で挿入ソートを行う」 というものです。n は要素数より小さい任意の数を n1 とした単調減少数列で、i → ∞ で ni = 1 に収束します （で良いのかな？）。言い方を変えれば、 「データを (n-1) 個飛ばしでピックアップできるだけピックアップして、 そのそれぞれを組にして挿入ソート」でしょうか。

31415926 -> 11234569
図(a): シェルソートの様子

動作例を図 (a) に示します。

で、この n の取り方によって、シェルソートの効率は O(n1.2) 〜 O(n2) で変動するらしいんですが、 効率の良い n について、あの D.E.Knuth 大先生が 「『 n1 = 1, ni+1 = ni * 3 + 1 』の 逆」という御神託を下さったそうなので、全面的に信用して採用しました。 つまり「1, 4, 13, 40, 121, ... 」の中から、要素数より小さい最大の数を n1 として、nn+1 = ( nn - 1 ) / 3 とすればいいわけです。

3. マージソート

これは、今まで出てきたソートとは違うタイプのアルゴリズムです。 「マージ (merge)」ってのは、「複数のものを混ぜ合わせて一つにする」 という意味だそうです。

で、その名の通り、「2 つのソート済みの配列を混ぜ合わせて、 1 つのソート済みの配列を作る」という方法でソートしていきます。 ですから、「混ぜ合わせる」前に一度「分割」しなければなりません。 ある程度のサイズまで分割されたら別のソート法でソートして、 マージソートで仕上げる、という方法がよく用いられる……らしいです。

31415926 -> 11234569
図 (b): マージソートの様子

やっぱり図で示した方が分かり易いので、そうすることにします。

図 (b) のように、配列を分割していくと、最終的に要素 1 つだけになりますが、 これを「ソート済みの配列」と見なせば (順番もクソも無いからね)、 マージソートだけでのソートも可能です。

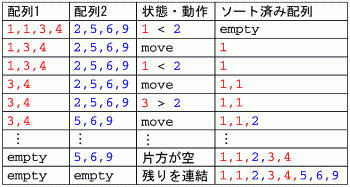
マージしながらソート
図 (c): マージしながらソート

「マージしながらソート」のやり方としては、それぞれの先頭を比較しながら、 マージしていく方法が考えられます。具体的には図 (c) のとおり。

この類のアルゴリズムを表す言葉として、 divide and conquer （ディバイド アンド コンカー: 分割して統治せよ） ってのが有りますが、かのローマ帝国の政治の方針がこれだったらしいです。

●実装

シェーカーソートはバブルソートを一寸弄ればすぐに実装できます。 シェルソートは挿入ソートで「1」である部分を「n (距離)」にするだけで実装できる ……はずだったのですが、前回の挿入ソートのソースではそれができません。(ぉ
以下のソースが「説明通りの」挿入ソートのソースです。挿入すべき部分を探す方法が違うだけで、 どちらもしっかり動きますので、そこの所はご心配なく。 

/* 「説明通りの」挿入ソート */
void
insertsort2(void *base, size_t nel, size_t width, int (*compar)(const void *x, const void *y))
{
    BYTE    *b = base, *tail, *ip, *jp;

    tail = b + ( nel - 1 ) * width;
    for( ip = b + width ; ip <= tail ; ip += width )
        for( jp = ip ; jp > b ; jp -= width )
            if( compar( jp - width, jp ) > 0 )
                swap( jp - width, jp, width );
            else
                break;
}

●サンプル

Cで書いてみたサンプル (download)
今回はさすがに単純なモノばかりでもないので、整数でカウントとかしてるものもあります。 ただ、逆に解りづらくなってる部分もあるかもしれません。悪しからず。

●備考

swap() を一寸高速化してみました。memcpy() が memmove() より速ければ、 速くなってるはずです。

今回はエラー処理を一寸簡単にするために、die() なる関数を組んで対応しました。 今まで一度もエラーが起こってないので正確には判りませんが、普通に呼んで動いたんで、多分問題無いと思います(ぉ

戻る