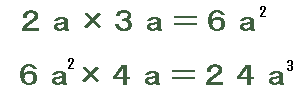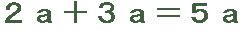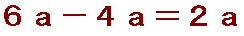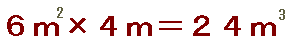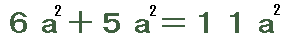嶼悢偲悢妛偱偐傢傞偲偙傠丅
偦偺戝偒側傕偺偺傂偲偮偵
倶傗倎側偳丄暥帤傪巊偆幃偺儖乕儖偑偁傝傑偡丅
俆亊倎偼俆倎偲彂偄偰偐偗嶼偺婰崋偼徣棯偡傞丄偲偐丅
偙偆偄偆偺偭偰丄儖乕儖傪妎偊偰偟傑偊偽
傗偭偰偄傞偙偲偼
彫妛惗偺帪偲偍側偠側偺偩偗傟偳丄側偐側偐偦偆偄偐側偄丅
俆亊倎亖侾俆偩偭偨傜丄乽倎偼俁偩偭乿偰傢偐傞偺偵
俆倎亖侾俆偩偲峫偊崬傫偱偟傑偆丅
椵忔丄偲偄偆偺偑偁傝傑偡傛偹丅
倶偺擇忔偲偐嶰忔偲偐丅
偁傟偵偟偰傕拞妛偱暥帤幃偺儖乕儖偑偱偰偒偰丄
偐偗嶼偩偭偨傜丄椺偊偽
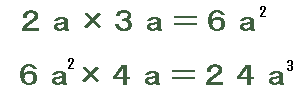
偺傛偆偵丄悢帤偼悢帤偱偐偗嶼丄暥帤偼偐偗偨夞悢偩偗俀忔丄俁忔丄偲
傆傗偟偰偄偔丅
偱傕
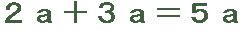
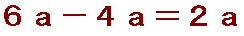
側偳偺傛偆偵
偨偟嶼傗堷偒嶼偩偲丄悢帤偺晹暘偩偗傪寁嶼偟偰暥帤偺晹暘偼曄傢傜側偄丅
傑偢丄偦偺傊傫偺偲偙傠偱偮傑偢偄偰偟傑偭偨傝丄
偳偭偪偩偭偨偐傢偡傟偪傖偭偰偙傫偑傜偑偭偨傝偡傞偺偱偡偑丄
偙傟傕幚偼拞妛峑偱弶傔偰傗偭偨傢偗偱偼側偄偺偱偡丅
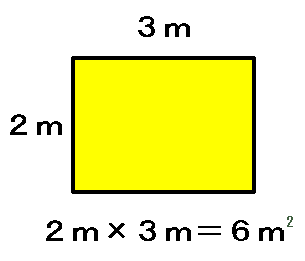
柺愊傪弌偡偲偒偼丄
偨偰亊墶
偙傟丄倎傗倶偑倣偲偄偆暥帤偵曄傢偭偨偩偗偱偡丅
偟偐傕撉傒曽偼噓乮暯曽儊乕僩儖乯
摨偠傕偺傪俀夞偐偗傞偙偲傪乽暯曽乿偭偰尵偆傫偩傛丄偭偰偙偲傑偱
偍偟偊偰偔傟偰偄傞傫偱偡丅
偝傜偵丄
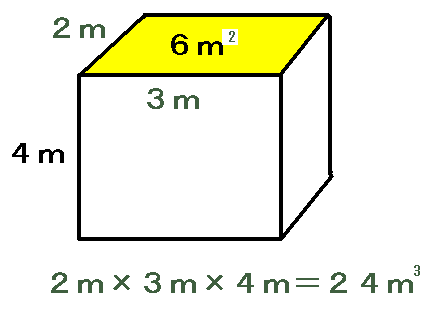
懱愊傪媮傔傞偲偒偼丄
偨偰亊墶亊崅偝
倣傪俁夞偐偗偰丄棫曽儊乕僩儖偲側傝傑偡丅乮棫曽懱偺棫曽偲摨偠偩偹乯
偙傟偼懠偺峫偊曽傪偡傞偲丄
傑偢乽偨偰亊墶乿傪偟偰柺愊傪弌偟偰偦傟偵乽崅偝乿傪偐偗偨丅
偮傑傝
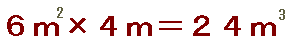
偲偄偆偙偲偵側傝傑偡丅
偙偺傛偆偵傒偰傒傞偲丄
偨偟嶼丄堷偒嶼偺偙偲傕丄側傫偺晄巚媍傕偁傝傑偣傫丅
俀倣亄俁倣亖俆倣
乮俀倣偲俁倣偺僸儌傪崌傢偣偰俆倣乯
俇倣亅係倣亖俀倣
乮俇倣偐傜係倣愗傞偲俀倣巆傞乯
摉偨傝慜偱偡傛偹丅
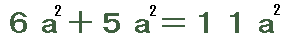
偼寁嶼偱偒傞偗傟偳丄
俇噓亄俆倣
偺傛偆偵暥帤偺晹暘偑偪偑偆傕偺偼丄
偦傟埲忋傑偲傔傜傟側偄丄偲偄偆偙偲傕
偙偺傛偆偵峫偊偰傒傞偲丄傢偐偭偰偔傞偲巚偄傑偡丅
偨偩摨椶崁偱偼側偄偐傜丄偱偼側偔偰
柺愊偲挿偝傪偨偟偰偟傑偭偨傜僿儞偱偟傚偆丠
側傫偲尵偄傑偟傚偆偐丅
偨偩傗傝曽偩偗傪妎偊偰栤戣偑乽偱偒偰偄偨乿偺偼
傎傫偲偆偵乽傢偐偭偰偄偨乿偺偲偼偪偑偆偺偱偡丅
傎傫偲偆偺棟夝偐傜晜偒忋偑偭偨偲偙傠偱
偨偩傗傝曽偵偟偨偑偭偰幃傪夝偄偰丄偙偨偊傪弌偟偰偄偨偩偗側偺偱偡丅
偩偐傜偪傚偭偲儖乕儖偑曄傢偭偨偩偗偱丄
偦傟偑慜偵偼乽偱偒偰偄偨乿傕偺偲寢傃晅偐側偄丅
拞妛峑偺曌嫮偑傢偐傜側偄偱彫妛惗偺乽嶼悢乿偵傕偳偭偰峫偊傞丄偲偄偆偺偼
乽抪偢偐偟偄乿偙偲偱傕側傫偱傕側偄丅
婎杮偺乽偒乿偵傕偳偭偰慜偵傗偭偨偙偲傪偟偭偐傝棟夝偡傟偽丄
崱傗偭偰偄傞妛峑偺曌嫮傕乽側乕傞傎偳丄偙偆偄偆偙偲傪尵偭偰偄偨偺偩側乿
偲側偭偰偔傞傕偺偱偡丅
傎傫偲偱偡傛丅
晧(儅僀僫僗)偺悢搊応偐傜丄惓晧偺悢偺寁嶼傊丅
曽掱幃偵栶棫偮儚儞億僀儞僩儊儌
拞妛惗偺儁乕僕
偼偠傔偺儁乕僕偵傕偳傞