運動のアニメーション　

高校生の皆さんへ
力や速度、加速度など、大きさと方向で表すベクトル量を簡単な実験やアニメーションを作成して理解しよう。
物体の運動には加速度運動と等速直線運動がある。
加速度運動は速さが変化したり、方向が変わったりする運動である。速さや方向が変化するのは力が働いているからである。
等速直線運動は一定の速さで、まっすぐ進む運動で、力が働かない運動である。
天体の引力や大気のない宇宙空間で物体を運動させると等速直線運動をする。止める力も働かないのでエネルギーは必要ない。

その１　等速円運動

　等速円運動は、物体が半径　r　の円周上を一定の速さで回る運動である。この運動は方向が変わるので,力（向心力）が働く加速度運動である。
１まわりするのにかかる時間を周期　T　という。
１秒間に動く中心角を角速度ωオメガといい、３６０度を２πradであらわす。したがって　ω=2π/T （rad/s)である。

ー実験ー
・飛ばしても危険がない消しゴムに糸を付けて円運動させてみよう。
・糸を放すと消しゴムはどの方向へ飛んでいくか、位置を変えて調べよう。

円運動させるには手に持つ糸を引いていなければならない。この中心の方向へ引く力を向心力という。
地球を回る人工衛星や月の向心力は引力である。
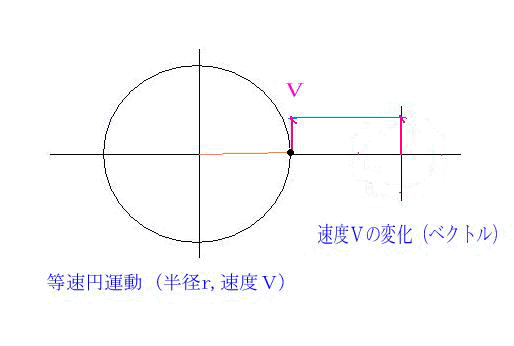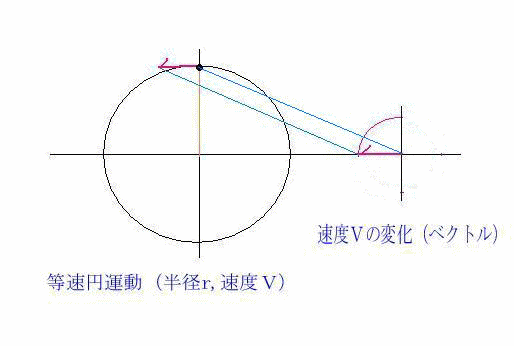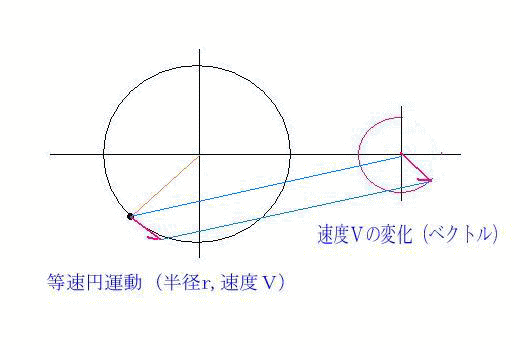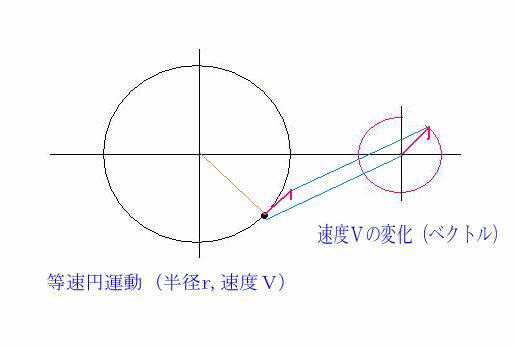
糸を放した瞬間、消しゴムは円の接線方向へ飛んでいくのが分かる。（速度Ｖは接線方向、アニメ参照）

ーアニメーショん作成ー

①パソコンにあるアクセサリーのペイントを使って、半径ｒの円及び接線方向の速度Ｖを平行移動した半径Vの８枚の図形を描く。枚数は多い方が滑らかな動きになる。
基本になる図形を描き、名前を付けて保存して置き、これに付け足すように描くと楽である。

アニメーション作成ソフトを使って、アニメーションにする。（ホームページ・ビルダーのウエブアニメーションを使用した。)
GIFアニメーションの無料ソフトもある。Giam http://homepage3.nifty.com/furumizo/

ー運動方程式ー
　
速さＶ,周期Ｔの等速円運動から(スカラー）
　　　　　
　　　　　Ｖ＝２πr/T・・・・・・（１）

等速円運動の加速度をαとする。加速度は速度の変化する割合である。
速度Ｖの変化（ベクトル）図形から、周期Ｔの間に円周２πＶ変化したことになる。
このようにベクトルの先端が描く線をホドグラフ（hodograph)という。

　　　　　α＝２πＶ／Ｔ・・・・・・（２）

（１）式と（２）式を使ってＴを消去する。

　　　　　α＝Ｖ²/ｒ・・・・・・・等速円運動の加速度

等速円運動している消しゴムの質量をｍとすると向心力は

　　　　　F＝ｍα＝ｍ　Ｖ²/ｒ
　
角速度ωを使う
ω＝２π/Tを使って（１）式、（２）式をあらわすと

　　　　　Ｖ＝２πr/T＝ｒω・・・・・・・・・・・（１）’
　　　　　α＝２πＶ／Ｔ＝Vω・・・・・・・・（２）’

　　　　　　α＝ｒω²

等速円運動している消しゴムの質量をｍとすると向心力は

　　　　　　F=mα=mｒω²

その２　円錐振り子

消しゴムをつるした長さLの糸が鉛直線と角度θをなして円錐を描きながら回転する運動が円錐運動である。

消しゴムに働く力は糸が引く力Sと地球が引く力ｍgの二つである。この二つの力の合力Fが向心力となって、消しゴムは円運動している。（ｇ　は重力加速度）
　　　　　　向心力　　F　=　ｍg　tanθ = m V²/r　＝S　sinθ

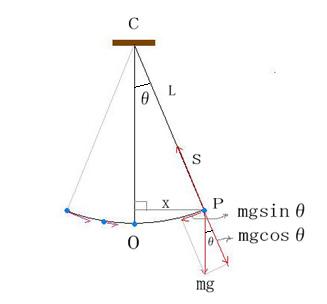
その３　単振り子

振り子を1つの面で振らせたものを単振り子という。振り子に働く力は重力（mg)と糸が引く力（S）の２つである。
重力mgをSの反対方向の力　mgcosθ, と接線方向の力　mgsinθに分解する。(下図）

　S－mgcosθ　は中心Cの方向へ働く向心力となり、短い時間でみると円運動になる。
　mgsinθ　は接線方向の力となり、振り子を振動させる。

単振り子の糸の長さ（L)と周期（T)の関係
振り子の振れを小さくすると、角θは小さく、おもりPのOからの水平距離xは円の弧OPとみることができる。
　　　sinθ＝x/L
接線方向の力 　mgsinθ=ｍｇ x/L 　となる。
加速度を　α　とすれば運動方程式は　F=mα=ｍｇ x/L　となる。したがって　a=ｇ x/L・・・・・（１）
この運動は半径xの単振動である。　　　α=xω²・・・・・（２）
（１）、（２）式から　ω²＝g/L　 したがって　　ω＝√g/L=2π/T 　(g/Lはルートの中）
　　　　　　　　　　　　　　　T=2π√L/ｇ　　　（L/gはルートの中)
単振り子の周期は糸の長さと重力加速度に関係している。

例えば振り子時計の周期、すなわち進み遅れは振り子の長さによって調整する。
地表の重力加速度は重力異常地域などあるが変化は少ない。
しかし、月面上の重力加速度は地球上の約6分の1である。月面探査機「かぐや」から月が注目されている。
入試に備えて計算してみよう。
問１　同じ長さの単振り子を月面へ持って行くと周期Tは地球の何倍になるか。
問２　地球上で正確な振り子時計を月面上へ持って行くと、長針が一周するのに何分かかるか。

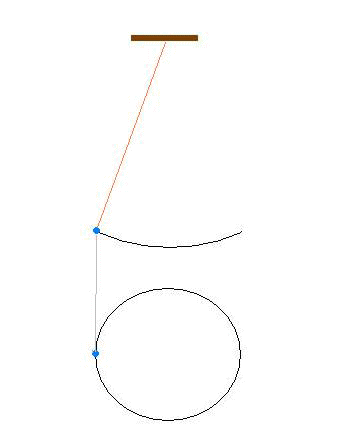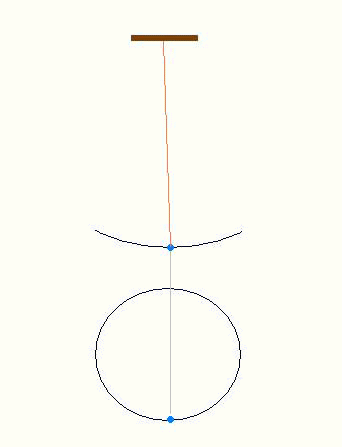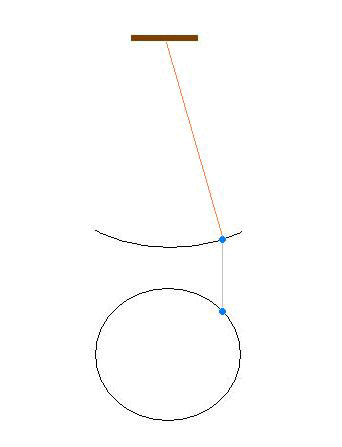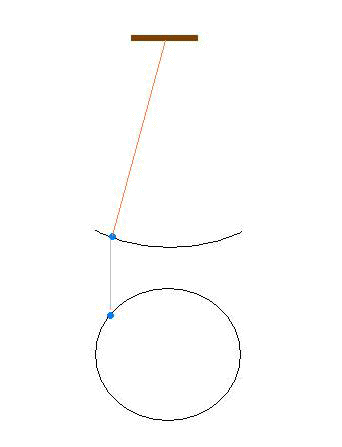
単振り子の位置エネルギーと運動エネルギーの関係
O点を基準にしたとき、P点にある質量mの物体が持っている位置エネルギーは E’＝ｍｇｈ＝ｍｇ（L－Lcosθ)
P点を初速０で振らせる。P点における運動エネルギーは０である。
物体がO点を通過するときの接線方向の速さをVとすると運動エネルギーは　E"＝ｍV²/2、位置エネルギーは０である。
エネルギー保存の法則から　　　　　ｍｇ（L－Lcosθ)=ｍV²/2　　となる。