高校生の皆さんへ

1.人工衛星の速さを求める式をつくって見よう。
　
　等速円運動している人工衛星の向心力を求めよう。
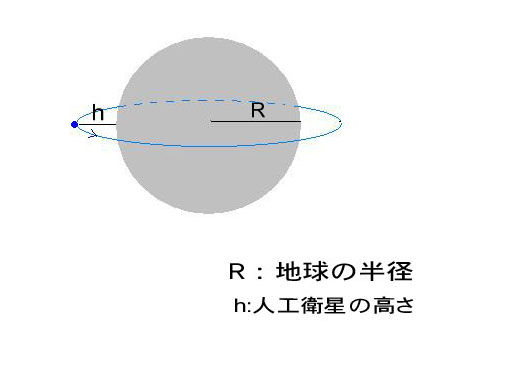
地球の質量Ｍ、半径Ｒとします。
人工衛星の質量 ｍ、人工衛星の地表からの高さ ｈ、人工衛星の速さ ｖ とします。

人工衛星の加速度　α＝ｖ²/(R+h)
運動方程式から向心力は
　　　　　　　　　　　　　　　　　Ｆ＝mα=m・ｖ²/(R+h)

地球と人工衛星の万有引力Ｆ’は比例定数をＧとすると
　　　　　　　　　　　　　Ｆ’＝Ｇ{Ｍ・ｍ/(R+h)²}

人工衛星が等速円運動する向心力 F は地球と人工衛星の万有引力（重力） F' です。(F=F')

　　　　　　　　　　　　m・ｖ²/(R+h)＝Ｇ{Ｍ・ｍ/(R+h)²}
　　　　　　　　　　　　
　　　　　　　　　　　　

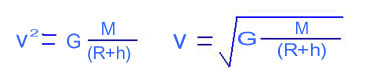
２．第一宇宙速度を求めてみよう。
高い山の上から水平方向へ物体を投げた場合を考えてみよう。
投げる物体の速さを増すと落下する地点はだんだん遠くなりますね。
ある速度 v になると落下せず、地球を一周してもとの位置へ戻ってきます。この速度 v を第一宇宙速度と言います。
この物体の質量をｍ、円運動の半径は地球の半径Ｒとします。（地球の半径に比較して山の高さは小さいので無視）
地表での重力加速度を ｇ とします。
物体の円運動の向心力Ｆは
　　　　　　　　　　　　　　　　　　　Ｆ＝ｍ・ｖ²/R
物体にはたらく重力Ｆ’は
　　　　　　　　　　　　　　　　　　　Ｆ’＝ｍｇ
Ｆ＝Ｆ’から
　　　　　　　　　　　　　　　　　　　ｍ・ｖ²/R　＝　ｍｇ
　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　∴　ｖ²＝Ｒｇ

問１　地球表面をすれすれに回る人工衛星の速さを求めてみよう。ただし、空気の抵抗は無いとします。地球の半径は６４０００００ｍ
重力の加速度ｇ＝９．８ｍ/s²とします。 (ｖ²＝Ｒｇを使う。答え　７．９　Ｋｍ／ｓ）

３．静止衛星について
ＢＳテレビの中継に使う人工衛星は地球の赤道上のある地点の上空に何時もあり、ＢＳテレビを見るパラボラアンテナもその方向へ向ければよい。このような人工衛星を静止衛星といいます。
静止衛星が地表のある地点の上空に静止しているように見えることについて考えてみよう。
地球は１日の周期で西から東へ自転していますので、静止衛星も同じ周期で同じ方向へ地球の周りを公転することになります。


問２．ケプラーの第三法則を応用して、静止衛星の公転半径 a を求めよ。また、静止衛星の速さを求めよ。
ただし、月が地球の周りを公転する周期を約２７日、月の公転半径を約３８００００Ｋｍ、静止衛星の公転周期を約１日とします。（２７＝３³）

（ a³/1² =380000³/27²　 a=42000Km,　　速さ v = 2πa/T　約３．１Ｋｍ／ｓ　）