地学を選択する高校生の皆さんへ

１．近い恒星の距離
基本は三角形の一辺（基線）と、2つの角度が分かれば、この三角形の全ての辺が分かるということです。（三角測量）
地球上離れた2つの天文台の距離を基線として、接近した小惑星の角度を望遠鏡で測定し距離を求めます。ケプラーの第３法則を使って、地球と太陽の距離をもとめます。詳しい説明は省略しますが，約1.5億ｋｍ（０．００００１５８光年）です。
地球と太陽の距離（ a ）を基線として、恒星の年周視差（ ｐ" ）を観測し、　ｄ＝３．２６/p　光年　　の式で恒星の距離（　ｄ　）を計算します。
（地球の自転と公転を参照）

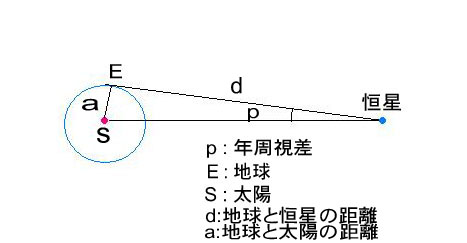
年周視差の説明図

d = 3.26/p 光年　の説明
年周視差 ( p" )は極めて小さな値です。地球と太陽と恒星の三角形を次のように考えます。
地球と太陽の距離　a　は恒星を中心とする半径ｄの円の弧と考えます。
中心角と弧の長さは比例するので、次ぎの比例式が出来ます。
　　　　　　　 　a/2πd =　p /360X60X60　　　　　 (360°を３６０Ｘ６０Ｘ６０”に変えた）
　　　　　　　　　∴　ｄ＝aX360X60X60/2πp　　　　　　　　　（１）

地球と太陽の距離　a＝０．００００１５８光年とπ＝３．１４を入れると

　　　　　　　　　　ｄ＝３．２６/p 　（光年）　　

問い。　シリウスの年周視差を　ｐ＝０．３７９”として、シリウスの距離を求めよ。（解答　８．６光年）