![]() 地学で受験する高校生の皆さんへ 作成途中
地学で受験する高校生の皆さんへ 作成途中
1.絶対等級と見かけの等星
恒星の真の明るさを比較するため、恒星を32.6光年(10パーセク)の距離に置いたときの等星を絶対等級といいます。
絶対等級はMであらわします。
見かけの等星がm等星、明るさが l 、年周視差がp”、距離dパーセクの恒星を
10パーセクの距離に持ってきたとします。絶対等級はM,明るさはL,年周視差は0.1”になります。
これらの関係式をつくってみます。
L/l = d²/10² =0.1²/p² (明るさは距離の2乗に反比例し、距離は年周視差に反比例します)
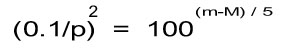
2( log0.1-logp ) = ( m-M )/5 log100
2(-1-log p ) = (m-M )2/5 ( log 0.1=-1 , log100=2 )
log p =0.2(M-m)-1
この式は見かけの等星mと絶対等級Mと年周視差pの関係式です。
絶対等級はスペクトル型やケフェウス型変光星の変光周期から正確な値ではありませんが、調べることができます。
遠くにあって、年周視差が観測できない恒星の距離を調べるのに使われます。
2.恒星のスペクトル型とヘルツスプルング・ラッッセル図
恒星のスペクトル型
恒星からの光をプリズムを使ってスペクトル分析すると、温度の違いによる吸収スペクトルの暗線が見えます。
吸収スペクトルの現れ方によって分類したのがスペクトル型です。
| スペクトル型 | 表面温度Kと色 | 特徴 | 例 |
|---|---|---|---|
| O型 | 25000以上、青 | ヘリウムイオンの暗線 | ケフェウス座λ |
| B型 | 15000 青白 | ヘリウム原子、水素の暗線 | スピカ |
| A型 | 8300 白 | 水素、カルシウムイオンの暗線 | シリウス |
| F型 | 6600 淡黄 | カルシウムイオン、水素、金属原子の暗線 | プロキオン |
| G型 | 5600 黄 | カルシウムイオン、水素、金属原子の暗線 | 太陽、カペラ |
| K型 | 4400 橙 | 金属原子の暗線 | アルデバラン |
| M型 | 3300 赤 | 金属原子の暗線、酸化チタンの分子の暗線 | アンタレス、ペテルギウス |
ヘルツスプルング・ラッッセル図(H・R図)
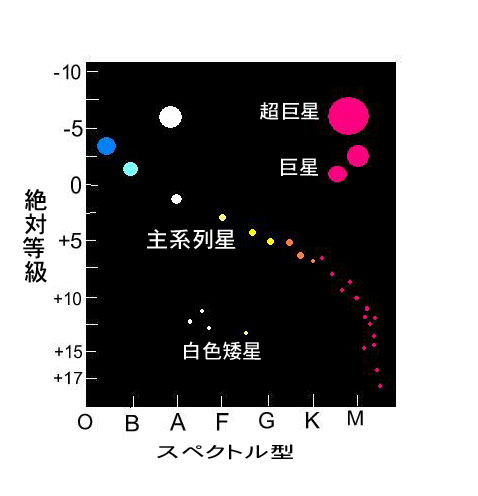
ヘルツスプルング・ラッセル図(H・R図 模式図)
ヘルツスプルング(デンマーク 1873年~)とラッセル(アメリカ 1877~)は年周視差が測定できる近くの星について,絶対等級とスペクトル型の関係を調べました。絶対等級を縦軸、スペクトル型を横軸にとり、恒星をプロットしたのがヘルツスプルング・ラッセル図です。(略して
HR図といいます )
主系列星
当然ではありますが、多くの恒星は左上から右下に分布し、温度が高いと絶対等級が明るくなります。
これらの恒星を主系列星といいます。太陽はG型で絶対等級が+ 4.8等級です。
巨星・超巨星
巨星・超巨星はK型やM型で温度は低く赤色ですが、直径が太陽の100倍とか1000倍も大きいため、絶対等級が明るいのです。
白色矮星
HR図の左下に分布する温度は高いけれど暗い星が白色矮星で、直径が太陽の100分の1程の小さい恒星です。
G型やK型の白色矮星もあるようです。
3.遠い恒星の距離の求め方
①スペクトル型から求める方法(分光視差)
年周視差が観測できない遠い恒星はスペクトル分析し、スペクトル型を調べ、ヘルツスプルング・ラッセル図から絶対等級Mを求めます。
見かけの等級mは観測できるので、 log p =0.2(M-m)-1から年周視差 p(分光視差という)を求め、次ぎにd=3.26/pで距離を求めます。
②脈動変光星(セフェイド)の周期光度関係から求める方法
恒星には膨張、収縮をくり返し、そのため明るさが変化する変光星があります。脈動変光星(セフェイド)といいます。
セフェイドの変光の周期と絶対等級の間に関係があり、周期光度関係と言います。
セフェイドの変光周期を観測し、周期光度関係から絶対等級を求め、 log p =0.2(M-m)-1から年周視差 p (セフェイド視差)を計算し距離を求めることが出来ます。