| あすみパソコンクラブは、元高校教師のグループで中学・高校用教育ソフトと理科教材の作成と配布をしております。 |
 |
| 面心立方格子と六方最密構造の新モデルの紹介 |
|
六方最密構造と面心立方格子の説明をするとき、図１や図２などを用いるが、それぞれ単独では理解できても、第３層目の重なり方による違いとしは、この２つモデルや図では理解しにくかった。 そこで、その違いを理解できる新しいモデルを作成してみた。 |
 図３ |
||
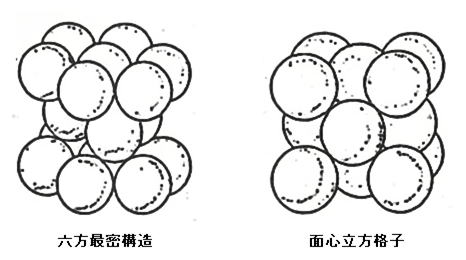 図１ |
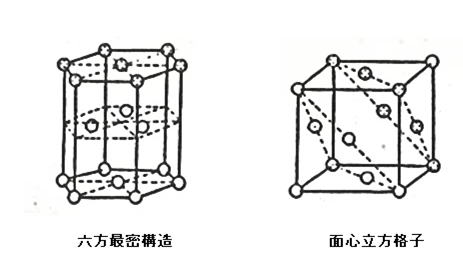 図２ |
||
| 新しいモデル（図３）では、直径５０ｍｍの発泡スチロール球を第１層目には３７個、第２層目には２７個、第３層目には１９個、合計８３個を並べ、木工用ボンドで接着した。 尚、第１層目と第２層目は固定し第３層目を動かせる様にし、六方最密構造と面心立方格子の違いをその断面で説明できる様にした。 また、第１層目と第３層目は白い発泡スチロール球を使用し、第２層目は青い発泡スチロール球を使用した |
|||
| 図４は、第２層まで積み上げた状態を上から見たところである、ここで重要なのは、第３層目を乗せることのできる位置が２種類あることに気づくことである。 図４の写真では分かりづらいので、図５の模式図で考えてみると Ｘ と Ｙ の２種類あることに気づく。 Ｘの位置は、第１層目の真上であり、Ｙの位置は第１層目、第２層目のどちらの位置とも一致しない位置である。 勿論、Ｘの位置に球を乗せると球の大きさの関係上、Ｙの位置には球を乗せることができない。 |
 図４ |
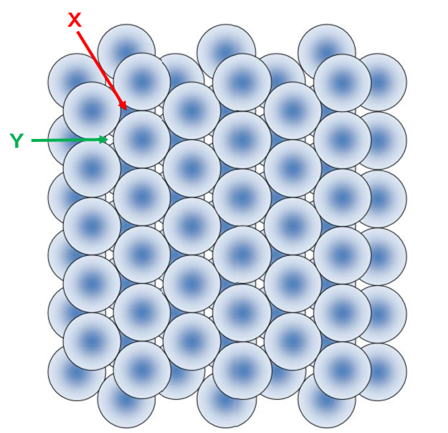 図５ |
||
|
その逆に、Ｙの位置に球を乗せると球の大きさの関係上、Ｘの位置には球を乗せることができない。 第３層目がＸの位置に乗れば、Ａ層、Ｂ層、Ａ層のＡＢＡＢの重なりで、六方最密構造になる。 第３層目がＹの位置に乗れば、Ａ層、Ｂ層、Ｃ層のＡＢＣの重なりで、面心立方格子になる。 |
| 次に、以上のことをもとに新しいモデルを使い六方最密構造と面心立方格子の違いをみていく。 図６が、第３層目が第１層目の真上の位置（Ｘの位置）に乗った状態のＡＢＡＢ（六方最密構造）である。 図７が、少しずれた位置（Ｙの位置）に乗った状態のＡＢＣ（面心立方格子）である。 図６と図７で第３層目がずれていることが確認できる。 |
 図６ |
 図７ |
| 第３層目が真上に乗せた状態である、図６を真上から切断すると、その切り口に現れるのが図８～図１０の六方最密構造である。 | |||
|
|||
|
図８ 図９ 図１０ |
|||
|
この時、図１０で分かる通り、第１層目と第３層目の球の切り口がともに半球であり、第１層目の真上に第３層目が乗っていることが確認できる。 |
|||
|
一方、図７は第３層目が第１層目の真上ではなく少しずれた位置に乗ったものである。 ずれていることを確認するために、これを真上から切断したものが、図１１図１２である。 図１２で分かる通り、第１層目と第３層目の切り口の形が異なったものになっている。 このことは、第１層目と第３層目がずれた位置であることを示している。勿論、第２層目の切り口とも異なっている。 |
 図１１ |
 図１２ |
||||
| この状態で斜めに切断すると、その切り口に現れるのが図１３～図１５の面心立方格子である。 なぜ、斜めに切断するのか分かりますか？ |
||||||
