

乷栤戣乸丂捀妏A偑俀侽亱偺擇摍曈嶰妏宍ABC偱佢ABE亖俀侽亱丄佢ACD亖俁侽亱偲側傞傛偆偵揰E,D傪偦傟偧傟曈AC忋丄曈AB忋偵偲傞丅偙偺偲偒佢DEB傪媮傔傛丅
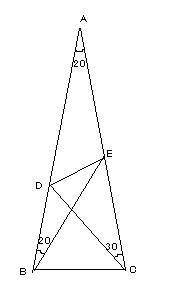
摎偊偼壓傊
伀
伀
伀
伀
伀
伀
伀
伀
伀
伀
 乷夝摎乸
乷夝摎乸
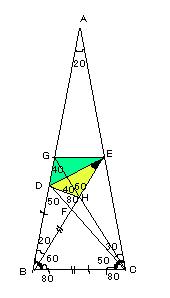 側偑偔側傞偺偱棯夝傪帵偟傑偡丅仮ABC偼捀妏俀侽亱偺擇摍曈嶰妏宍偩偐傜俀偮偺掙妏偼俉侽亱偩偐傜丄
側偑偔側傞偺偱棯夝傪帵偟傑偡丅仮ABC偼捀妏俀侽亱偺擇摍曈嶰妏宍偩偐傜俀偮偺掙妏偼俉侽亱偩偐傜丄
佢EBC亖俇侽亱丄佢DCB亖俆侽亱
仮BCD偵偍偄偰丄佢CDB亖侾俉侽亱亅乮俉侽亱亄俆侽亱乯亖俆侽亱
偩偐傜丄佢DCB亖佢CDB傛傝BD亖BC.....嘆
(曗彆慄傪傂偔乯E傪捠傝曈BC偵暯峴側捈慄傪堷偒曈AB偲偺岎傢傝傪G偲偟丄B偲E丄C偲G傪寢傃岎揰傪H偲偡傞丅
仮HBC偼BH亖CH偺擇摍曈嶰妏宍偱偐偮佢HBC亖俇侽亱偩偐傜仮HBC偼惓嶰妏宍丅摨條偵仮HEG傕惓嶰妏宍丅備偊偵丄BH亖BC.....嘇
仮BDH偵偍偄偰丄嘆嘇傛傝BD亖BH丄佢DBH亖俀侽亱偺擇摍曈嶰妏宍偩偐傜掙妏佢BHD亖俉侽亱
佢GHE亖俇侽亱偩偐傜佢DHG亖侾俉侽亱亅(佢BHD亄佢GHE)亖係侽亱.....嘊
仮BCG偵偍偄偰丄佢BGC亖侾俉侽亱亅乮佢GBC亄佢GCB乯亖係侽亱.....嘋
仮DGH偵偍偄偰丄嘊嘋傛傝DG亖DH.....嘐
仮EGH偼惓嶰妏宍偩偐傜EG亖EH.....嘑
仮DGE偲仮DHE偵偍偄偰
嘐丄嘑丄DE嫟捠偺嶰曈憡摍偵傛傝丄仮DGE佭仮DHE丂傛偭偰佢GED亖佢HED
佢GEH亖俇侽亱偩偐傜佢BED亖佢GEH亐俀亖俁侽亱.....(摎乯
偙偺栤戣傪侾侽擭偖傜偄慜偩偭偨偲巚偆偑丄庴尡傪峊偊偨拞妛惗傪傕偮恊偐傜丄夝偄偰偔傟偲偨偺傑傟偨丅忋偺棯夝偼丄側偐側偐夝偗偢俁擔栚偵傗偭偲傒偮偗偨巹偺夝摎偱偡丅悢擭屻丄怴挭暥屔偺乽偍偐偟側偍偐偟側悢妛幰偨偪乿乮栴栰寬懢榊挊乯傪撉傫偱偄偨傜傎偲傫偳摨偠栤戣偺夝朄偑嵹偭偰偄傞偺傪傒偮偗傑偟偨丅埳摗岹挊偺乽悢妛僩儗乕僯儞僌乿偵傕丄巹偼傒偨偙偲偼側偄偑丄嵹偭偰偄傞偦偆偱偡丅巹偺夝朄偲偼曗彆慄偺堷偒曽偐傜堎側傝丄嵟屻偵丄巹偼嶰妏宍偺崌摨傪偮偐偆偺偵懳偟丄怴挭暥屔偺傎偆偼丄墌偺墌廃妏偲拞怱妏偺娭學傪巊偭偰偄傑偟偨丅側傞傎偳拞妛惗偵夝偗傞掱搙偺傕偺偱偟偨丅








 側偑偔側傞偺偱棯夝傪帵偟傑偡丅仮ABC偼捀妏俀侽亱偺擇摍曈嶰妏宍偩偐傜俀偮偺掙妏偼俉侽亱偩偐傜丄
側偑偔側傞偺偱棯夝傪帵偟傑偡丅仮ABC偼捀妏俀侽亱偺擇摍曈嶰妏宍偩偐傜俀偮偺掙妏偼俉侽亱偩偐傜丄
