![]() 崅峑惗偺奆偝傫傊
崅峑惗偺奆偝傫傊
侾丏楢惎偺塣摦偐傜媮傔傞丅
俀偮埲忋偺峆惎偑枩桳堷椡傪媦傏偟側偑傜塣摦偟偰偄傞峆惎傪楢惎偲偄偄傑偡丅楢惎偺悢偼懡偔丄慡峆惎偺俁暘偺侾偼楢惎偩偲偄傢傟偰偄傑偡丅
壓恾偺傛偆偵丄柧傞偄庡惎偲埫偄敽惎偺塣摦傪挷傋偰傒傑偡丅
庡惎偲敽惎偼嫟捠廳怱俷偺傑傢傝傪偍屳偄偵岞揮偟偰偄傑偡丅幙検傗嫟捠廳怱傑偱偺嫍棧偺娫偵偼師偓偺娭學偑偁傝傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俵乮倎亅倱乯亖倣倱丂丂丂丂丂丂丂亪丂倱亖俵a乛(M+m)丒丒丒丒丒丒嘆
丂
敽惎偺妏懍搙傪冎乮rad/s)丄岞揮廃婜傪俹乮倱乯偲偡傞丅墌塣摦偺壛懍搙偺戝偒偝偼丂s冎²丂偱偡偐傜
敽惎偺岞揮偵傛傞岦怱椡丂俥e偼
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俥倕亖ms冎²丂亖ms (2兾/P)²丂
敽惎偲庡惎偲偺堷椡丂俥偼枩桳堷椡偺掕悢傪俧偲偡傞偲
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂俥亖俧(Mm/a²)
敽惎偺岦怱椡偼敽惎偲庡惎偲偺堷椡偱偡偐傜
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂ms (2兾/P)²亖俧(Mm/a²)丂丒丒丒丒丒丒丒丒丒丒丒嘇
嘇幃傊嘆幃傪戙擖偟偰倱傪徚偟傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂a³/P² = G(M+m)/4兾²
嬤偔偺楢惎偱庡惎偲敽惎偺嫍棧a偲敽惎偺岞揮廃婜俹偑娤應偱偒傟偽丄庡惎偲敽惎偺幙検偺榓乮俵亄倣乯傪媮傔傞偙偲偑弌棃傑偡丅
傑偨嫟捠廳怱傑偱偺嫍棧倱傪娤應偡傟偽嘆幃傪巊偭偰俵偲倣偵暘偗傞偙偲偑弌棃傑偡丅
偙偺傛偆偵嬤偔偺楢惎偱媮傔偨幙検偲愨懳摍媺乮峆惎偺恀偺柧傞偝乯偺娫偵娭學偑偁傝傑偟偨丅乮幙検岝搙娭學乯
峆惎偺幙検偑戝偒偄傎偳丄壏搙偑崅偔丄曻弌偟偰偄傞岝偺僄僱儖僊乕偑懡偄偺偱偡丅乮俫俼恾偺庡宯楍惎乯
俀丏墦偔偺峆惎偺幙検偺媮傔曽
峆惎偺僗儁僋僩儖宆傪娤應偟丄俫俼恾偐傜愨懳摍媺傪媮傔傑偡丅偦偺愨懳摍媺傪巊偭偰丄乽幙検岝搙娭學乿偐傜幙検傪媮傔傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
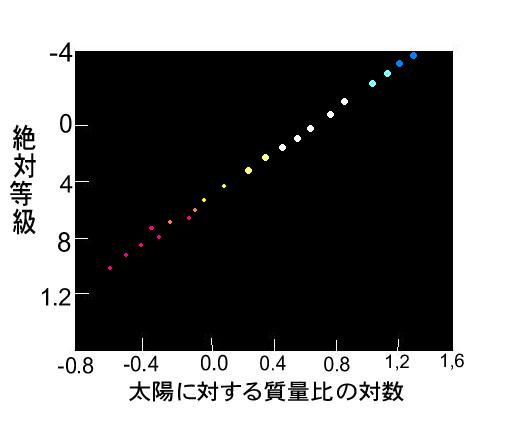
幙検岝搙娭學
墳梡丂a³/P² = G(M+m)/4兾²傪懢梲宯偺榝惎傊
懢梲偺幙検傪俵偲偟丄懢梲偺傑傢傝傪岞揮偡傞榝惎偺幙検傪倣偲偟傑偡丅
榝惎偺幙検倣偼懢梲偺幙検俵偵斾妑偟偰旕忢偵彫偝偄偺偱柍帇偱偒傑偡丅偟偨偑偭偰丄嫟捠廳怱俷偼懢梲偺拞怱偵偁傞偲偟傑偡丅
懢梲偲偦傟偧傟偺榝惎偺嫍棧傪a,岞揮廃婜傪俹偲偡傞偲丄幃偼師偺傛偆偵側傝傑偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂a³/P² = GM/4兾²
偙偺幃偺塃曈偼榝惎偵娭學偺側偄堦掕側抣偱偡丅
榝惎偺懢梲偐傜偺嫍棧 a 偺俁忔傪丄偦偺榝惎偺岞揮廃婜 俹偺俀忔偱妱傞偲堦掕側抣偵側傞偲偄偆偙偲偱偡丅
偙傟偼働僾儔乕偑娤應帒椏偐傜媮傔偨働僾儔乕偺戞俁朄懃傪帵偟偰偄傑偡丅
栤丂懢梲偲抧媴偺嫍棧傪侾偲偡傞扨埵傪揤暥扨埵偲偄偄傑偡丅懢梲偲搚惎偺嫍棧傪俋丏俆俆係揤暥扨埵偲偟丄岞揮廃婜傪俀俋丏係俇擭偲偟偰丄
丂丂丂働僾儔乕偺戞俁朄懃偑惉傝棫偮偙偲傪妋傔偰傒傛偆丅乮僸儞僩抧媴偺岞揮廃婜偼侾擭偱偡丅乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂![]()