一筆書きができるかどうか判定する方法を説明します. わかりやすく説明する代わりに, 理論的に厳密でないところもあります. また, この分野は私の専門でないことをはじめにお断りしておきます.
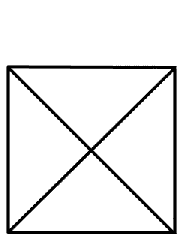
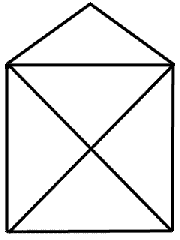
上の左の図形は一筆書きできませんけれど, 右の図形は一筆書きできます. それはどうしてわかるのでしょうか.
線で描いた図に対して, 図の上の各点に対して 点の 位数 (次数ともいう) と いう数値があります. そして位数が奇数の点を数え上げると, 一筆書きできるかどうかわかります. それでは位数とは何でしょうか.
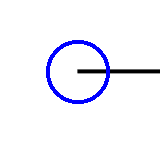位数を知りたい点を中心に小さな円を描いてみます.
そして, 円周が図の線と交わるところがいくつあるか数えます.
交点の個数が位数です. いくつか例を挙げましょう. 線の端の点の位数は1です.
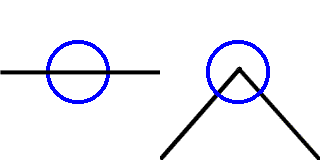
線の途中の点の位数は2です. まっすぐでも
折れていてもカーブしていても同じです.
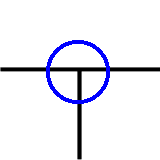
丁字路のようになっている点の位数は3です.
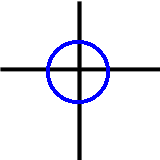
十字路になっていれば位数は4です.
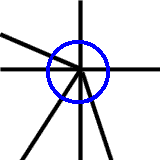
これは位数7の点の例です.
さて, 小さい円を描くと言いましたが, どのくらい小さければいいのでしょうか. 厳密にいうと, 円を限りなく小さくしたときの交点の個数の極限値が位数です. 例えば線分の端の点は位数1ですが, 端以外の点は端にどんなに近くても位数2です. [位数がわかったら 次へ]