敧昐壆偝傫偱楢棫曽掱幃傪峫偊傞
丂丂俁倎亄俀倐亖俀侾乧嘆
丂丂丂倎亄俀倐亖侾侾乧嘇
丂椺偊偽忋偺傛偆側楢棫曽掱幃偼丄
傑偢幃嘆偐傜幃嘇傪堷偄偰丄
丂丂俁倎亄俀倐亖俀侾乧嘆
亅乯丂倎亄俀倐亖侾侾乧嘇
丂丂 俀倎 亖侾侽丂椉曈傪俀偱傢偭偰
丂丂丂丂丂倎丂丂丂亖俆
偙傟傪幃嘇偵戙擖偟偰
丂丂丂俆亄俀倐亖侾侾
丂丂丂丂丂俀倐亖侾侾亅俆
丂丂丂丂丂俀倐亖俇
丂丂丂丂丂丂倐亖俁
摎偊丂倎亖俆丄倐亖俁
偲偄偆傛偆偵偟偰夝偄偰偄偔傢偗偩偑丄偙傟傪倎乮傝傫偛乯倐乮僶僫僫乯偲
抲偒姺偊偰峫偊偰傒傞偲師偺傛偆偵側傞丅

忋偺僷僢僋偑儕儞僑俁偙僶僫僫俀杮偱俀侾墌丅乮傗丄埨偄乯
壓偺僷僢僋偑儕儞僑侾偙僶僫僫俀杮偱侾侾墌丅乮偙傟傑偨埨偄乯
丂偱偼側偤抣抜偑堘偆偐偲偄偆偲丄忋偺曽偑儕儞僑偑俀偙懡偄偐傜偱
傝傫偛俀偙偱侾侽墌偩偐傜傝傫偛偼侾偙俆墌丄僶僫僫偼俁墌偲偄偆偙偲偵側傞丅乮埨偄側偁乯
丂丂俁倎亄俀倐亖俀侾乧嘆
丂丂俀倎亄丂倐亖侾俁乧嘇
偺傛偆側応崌偩偲壓偺嘇偺幃傪俀攞偟偰
丂丂俁倎亄俀倐亖俀侾
亅乯係倎亄俀倐亖俀俇丂忋偺幃偐傜壓偺幃傪堷偔偲
丂丂亅丂倎丂丂丂亖亅俆
丂丂丂丂倎丂丂丂亖丂俆
偙傟傪嘇偵戙擖偟偰
丂丂俀亊俆亄倐亖侾俁
丂侾侽亄倐亖侾俁
倐亖侾俁亅侾侽
丂丂丂丂丂丂倐亖俁
摎偊丂倎亖俆丄倐亖俁
偲偄偆傛偆偵偟偰夝偔傢偗偱偙傟傕儕儞僑僶僫僫偵抲偒姺偊偰偟傑偆偲丄

偲側偭偰偙傟偩偲抣抜偺斾妑偼偱偒側偄偺偩偑丄偦偙偱
壓偺僷僢僋傪傕偆傂偲偮攦偭偰儕儞僑係偮丄僶僫僫俀杮偱俀俇墌偵偟偰傒傞偲
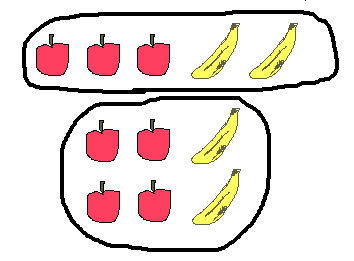
儕儞僑侾偙偺堘偄偱俆墌偲摎偊偑弌傞偲偄偆傢偗偱偁傞丅
丂傕偪傠傫楢棫曽掱幃偱偼椉曽偺幃傪壗攞偐偟偨傝彫悢傗暘悢偺摎偊偑弌偨傝偲傕偭偲暋嶨側僷僞乕儞傕弌偰偔傞偺偩偑丄梫偼曅曽偺暥帤偺學悢傪偦傠偊偰徚偡偲偄偆偙偲偱偦傟偝偊偟偭偐傝棟夝偟偰偄傟偽屻偼寁嶼偺傗傝曽傪妎偊偰僾儔僗儅僀僫僗偝偊傑偪偑偊側偗傟偽俷俲偱偁傞丅
師傊
拞妛惗偺儁乕僕偵傕偳傞
偼偠傔偺儁乕僕偵傕偳傞


