T's Page｜カーブのことについて（カーブってなに？）

１．カーブってなに？

　前のページで述べたとおり、地形に沿った道路を作ろうとすると、曲線（カーブ）が必要になってきます。
　でも、やみくもに地形なりにカーブを設置しているわけではありません。全国どこでも一定のルールに従って道路（カーブ）は設置してあります。

1.中心線について
　道路は、それが何車線であろうと基本的には一本の線から成り立っています。この基本になる線を中心線（センターライン）と呼びます。
地形に沿ってルートを計画した場合、中心線はどこかで曲がることになります。曲がる前の直線と曲がった後の直線の交点をI.P.（アイピー：インターポイント）と呼びます。そして、交差する角度をI.A.（インターアングル）で表します。

2.カーブについて
　I.P.でいきなり曲がろうとしてもスピードの出ているクルマにしてみたら、なかなかスムーズに曲がることはできませんし、クルマの構造上ハンドルを切って曲がるときには常に曲線を描いて曲がっています。
　そこで、より走りやすくするために2本の直線を曲線でつなぐことにしました。この曲線には次のような種類のものが用いられます。

			┌─	単曲線
	┌	円曲線	─┼─	複合曲線
曲　線	─┤		└─	反向曲線
	│		┌─	３次放物線
	└	緩和曲線	─┼─	レムニスケート
			└─	クロソイド

　ここでは、一般的に用いられる円曲線のうち、単曲線について話を進めます。
この1つのI.P.に対して1つの円を持ったカーブを単曲線と呼びます。円の大きさはR（半径）で表します。もちろんRが大きいほどカーブは大きくなるため、より高いスピードで曲がることができます。しかし、I.A.が同じ場合、Rを大きくするとカーブの長さ（C.L.）が長くなり、カーブを曲がっている時間も長くなるため、結果的に横Gを受ける時間も長くなります。

単曲線の諸要素

ＩＰ：交点
ＩＡ：交角
　Ｒ：半径
ＢＣ：単曲線の始点
ＥＣ：単曲線の終点
ＴＬ：接線長＝Ｒ×tan（ＩＡ／２）
ＣＬ：曲線長＝Ｒ×ＩＡ°／ρ°　　ρ°＝１ラジアンの度数＝１８０／π
ＳＬ：外線長＝Ｒ×（sec（ＩＡ／２）－１）

3.安全に走行できるカーブを作る
　カーブを走行するとき、速度によっては横滑りを起こしたり、あるいは遠心力に対する安全性からクルマはどうしてもカーブの内側を走行しがちです。そのため、カーブの内側へ向かって下り勾配をつけたり（片勾配）、道路幅を広げたり（拡幅）します。
　片勾配については、直線中では外側へ向かって下り勾配がついています。これは路面の排水が主な目的です。カーブ中ではＲの中心点方向に下り勾配をつけます。自動車自身の重力と遠心力の合成力が路面に対してより垂直側へ働くようになる（グリップが増す）ことから、より安全に走行できるようにするためです。
　拡幅は、自動車が内輪差を持っていることから、Ｒが小さくなるほど大きな量の拡幅をカーブの内側へつけてやります。
　また、カーブ中に限らず進行方向に対して、勾配の変化するところでは、カーブと同じ理由で走りやすくするため、かつその先の見通しをよくするために曲線（縦断曲線）を入れてやります。
　また、これらのカーブに対する設計上の技術的な基準が道路構造令という法令に定められています。機会を見てこの道路構造令についても紹介したいと思っています。

片勾配（これは直線中の絵です。）

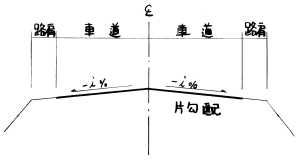片勾配は、基本的にはセンターラインを頂点として路肩側へ向かって下がる勾配をつけます。
カーブ中では、センターラインより内側車線ではマイナスの、外側車線ではプラスの勾配をつけます。
単曲線の場合、ＢＣで片勾配が最大となるようＢＣ手前の直線中に緩和区間を設けてすりつけます。

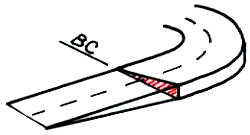カーブ中の片勾配のイメージ

拡幅

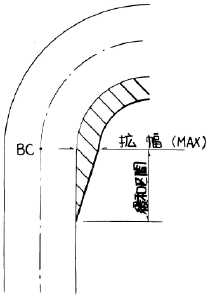　拡幅は、一般道路の場合内側の車線に二車線分まとめてつけるのが一般的です。現場におけるセンターライン（白や黄色の線）は、全体の幅員を二等分した位置に入れられます。
　単曲線の場合、ＢＣで拡幅量が最大となるようＢＣ手前の直線中に緩和区間を設けてすりつけます。

次（クロソイド曲線）