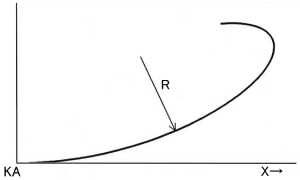２．クロソイド曲線

	クロソイド曲線のイメージ：Ｌが大きくなるほどＲが小さくなる。
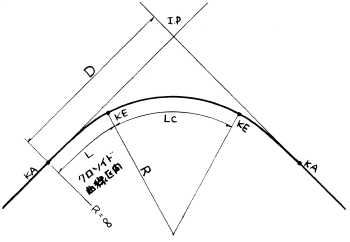	クロソイド曲線の諸要素 ＫＡ：クロソイド始点 ＫＥ：クロソイド終点 　Ｒ：ＫＥにおける曲率半径 　Ｌ：クロソイド曲線長 Ｌｃ：円曲線長 　Ｄ：接線長 　定数のＡをパラメーターと呼びます。 　ＲとＬを決定すると、自動的にＡの値も決定されるわけですが、Ｒ／３≦Ａ≦Ｒであることが望ましいとされています。 　したがって、道路の中心線（ＩＡ）とＲ、Ｌ、Ａのうち一つの要素が決まれば、残りの要素については、さほど選択の余地がないことになります。
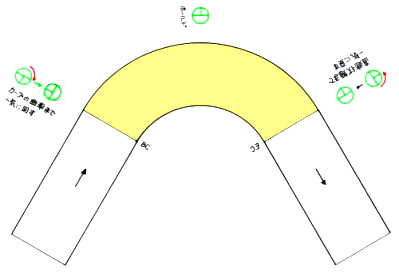	単曲線のカーブの始まりでは、曲率がいっきに変わるため、ステアリングも曲率に合わせて一気に切らなくてはなりません。
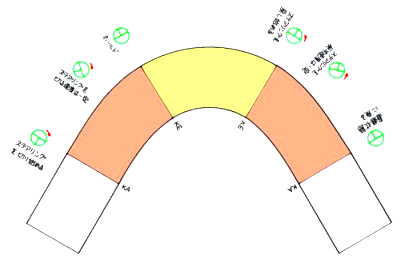	クロソイド曲線中は、そのカーブの最大曲率に至るまでに徐々に（等速で）ステアリングを切って行けばよいので、スムーズかつ安全に走行できます。

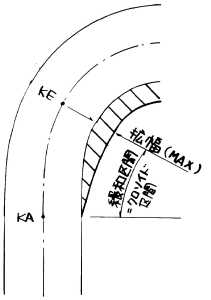実際にはクルマの幅は車線の幅より相当狭く、車線中のどこでも走ることができるわけですから、あまり現実味を持たない話ですが、建設時の合理性を考えるとやはりクロソイドはあらゆる意味でとても優れています。特に高速化してきた交通の流れの中では安全性の面からみても重要になります。建設現場の施工管理はたいへんですが。 　さて、このクロソイドにおける拡幅のすりつけ方ですが、別のクロソイドを入れる方法や、高次の放物線を使う方法などがあります。このうち別のクロソイドを入れるのは、都市部の高速道路などで用いられる方法です。一般的には高次の放物線を入れます。 　この放物線における拡幅量は 　Ｗｎ＝（４a＾３−３a＾４）Ｗ　 　　a＝Ｌi／Ｌ 　　Ｗn：任意の点の拡幅量 　　Ｗ：KE点における最大拡幅量 　　Ｌｉ：ＫＡ点より任意の点までの曲線長 　　Ｌ：クロソイド全区間の曲線長 で表されます。