 「ケーニヒスベルクの七つ橋」
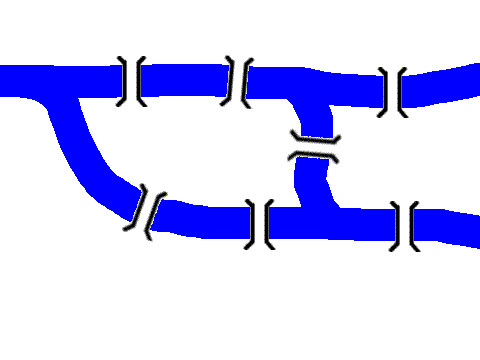
「ケーニヒスベルクの七つ橋」一筆書きの問題を数学的に考えたのはスイス生まれの数学者オイラー (Leonhard Euler, 1707-1783) です. 彼がケーニヒスベルク (いまのカリーニングラート) にいたころ, 「橋渡りの問題」というクイズが町で流行ってました. この地図 (地形を精確に描いたものではありません) のように 七つの橋が架かっているのですが, 七つの橋すべてをちょうど一回ずつ 渡る道順を探し求める問題です.
 「ケーニヒスベルクの七つ橋」
「ケーニヒスベルクの七つ橋」
一筆書きの問題を数学的に考えたのはスイス生まれの数学者オイラー
(Leonhard Euler, 1707-1783) です.
彼がケーニヒスベルク (いまのカリーニングラート) にいたころ,
「橋渡りの問題」というクイズが町で流行ってました.
この地図 (地形を精確に描いたものではありません) のように
七つの橋が架かっているのですが, 七つの橋すべてをちょうど一回ずつ
渡る道順を探し求める問題です.
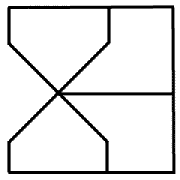 オイラーはケーニヒスベルクの橋渡りの問題が
左の図形を一筆書きするのと同じであることに気づき,
一筆書きの問題として考察しました.
そして, 前に述べた判定法を発見し,
七つの橋を一回ずつ渡る道順のあり得ないことを示しました.
5位の点が一つ, 3位の点が三つあり, 奇数位の点は合計4個ですね.
オイラーはケーニヒスベルクの橋渡りの問題が
左の図形を一筆書きするのと同じであることに気づき,
一筆書きの問題として考察しました.
そして, 前に述べた判定法を発見し,
七つの橋を一回ずつ渡る道順のあり得ないことを示しました.
5位の点が一つ, 3位の点が三つあり, 奇数位の点は合計4個ですね.
図形が一筆書きできるかどうか考えるときに, 長さとか面積とか 角の大きさとかいう量の概念は関わりがなく, 線がどうつながっているか つながり方だけが問題です. 専門的な用語でいえば位相 (topology) が問題なのです. オイラーがケーニヒスベルクの橋渡りの問題を考えたことで, 幾何学は量の概念から解放され, つながり方つまり位相を論ずる幾何学が生まれました. 位相の概念は現代数学の中で最もたいせつな概念の一つです. 量の概念に縛られずに構造を考えることは, 幾何学に限らず, 現代数学の全般にわたる特徴です. [終]