 78分法(シチハチブンポウ)とは?利息は、本来毎回つどの元本残に対応して計算され、 78分法(シチハチブンポウ)とは?利息は、本来毎回つどの元本残に対応して計算され、
結果的 にその合計額が利息合計額になるわけです。
しかしここで アドオン方式等により、既に利息合計額
が求められているもの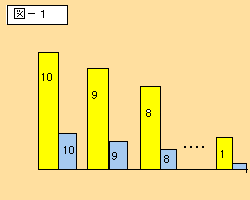 に対して、その後一括清算等に に対して、その後一括清算等に
よる利息割り戻しの為の毎回 支払いの利息を
考えた場合、本来であれば実質年率計算で
元利 内訳の計算をして、その未経過利息を
戻す形となるものです。
しかし、その計算は非常に煩雑でコンピュータ等で
なければ 容易に計算はできません。
そこで、利息戻し計算が実質年率 計算に比較的
近いもので、かつ簡単に計算ができる方法として
あるのがこの「78分法」なのです。
これは、毎回次の利息を単純に平均化して
考えられたもので、 利息合計額を回数の
総和数(10回であれば 55)で割ったものを
1つの "ます目" として、当初回数分
積み上げたます目を 支払を1回する毎に"ます目"
(平均的利息)が1つ減っていく 考えなのです。
元本残(図−1の黄色部分)が均等に1/10づつ
減っていくとすれば、 利息は元本残に対応したもの
として、同じように1/10づつ減って いく形となります。
図−1の利息部分(青色部分)を抜き出したものを
図−2として
次の具体例で説明します。
| 例 題 |
10回均等払いで、5回まで支払った直後、早期一括清算をする
場合の戻し利息(未経過利息)は? |
1回支払する毎にます目(利息)が1つ減るものとして、
回ごと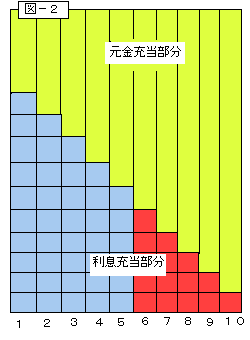 に残回数分だけ積み上げたものの総和を利息 に残回数分だけ積み上げたものの総和を利息
合計額とした場合 右図のようになります。
(青と赤の部分が利息合計額になります。)
つまり、図のように平均的利息を1つのます目と
考えた場合、 10回払いであれば、
1回支払う毎に1個づつます目が減っていき、
10回目支払後に利息もゼロになるというものです。
この場合(10回払)、そのます目の総数は
1+2+3・・・・+10=55個 であり、
5回まで支払った 直後の未経過利息(赤色)は
15個分ということに なります。
つまり、この時点で早期一括清算するとすれば、
利息合計 55の内15を戻すということになります。
これは、言い換えると、
利息合計を55等分した内の 15分を戻す、
つまり
戻し利息=利息合計額×15/55 ・・・・(A)
となります。
これを、数式にあてはめてみた場合、等差数列の公式を
含む形となります。
等差数列の公式
前述の 1+2+3・・・・+10=55 は増分1づつの
等差数列であり、 回数分のます目の個数(=総和数)
は等差数列の公式で求められます。
1+ 2+ 3+ 4+ 5+ 6+ 7+ 8+ 9+10
+ + + + + + + + +
+
10+ 9+ 8+ 7+ 6+ 5+ 4+ 3+ 2+
1
↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
11+11+11+11+11+11+11+11+11+11=110
(10+1)=(9+2)=(8+3)・・・・・・・ となり、
その合計は、和が等しい(この場合11)群が、10項で11×10=110
そして、2回加算している形なので、110/2=55 となります。
つまり、11×10/2=(初項+最後項)×項数/2
回数×(回数+1)/2=55 ・・・・・・総和数 となります。
ここで、早期一括清算による戻し利息を考えた場合、前述の(A)の式に
あてはめると、
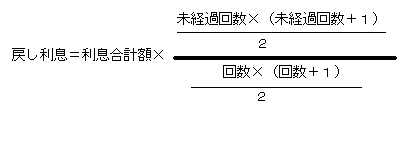 となります。 となります。
クレジット会社等での利息戻し計算は、この78分法が多く使われていますが
この計算はあくまで金利だけの計算であり、金利の他にいろいろの経費
(例えば、調査費や事務手数料あるいは請求の費用等)がかかっている為
その一部の負担を戻し利息から差し引きする場合があります。
年率を考えるとき、年率は年であるので、一年を12回(月払)でみた場合
その平均的利息(ます目)の個数は、等差数列の総和により
"78" になるので
78分法といわれるものです。
|
|
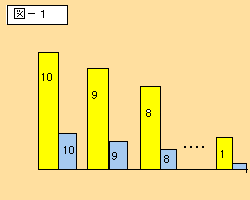 に対して、その後一括清算等に
に対して、その後一括清算等に に残回数分だけ積み上げたものの総和を利息
に残回数分だけ積み上げたものの総和を利息